NEUROBACK: IMPROVING CDCL SAT SOLVING USING GRAPH NEURAL NETWORKS
が公開になっています。未だソースは公開になっていないようですが、５％－７％の性能向上が見られたということのようです。本当にこんな単純なことで、そんなに性能向上するのか？の疑問に答える形の論文になっています。
ソースが公開されたら、データセットも整備されているので、やってみようと思います。
スケジュールナースでのプロジェクト群を同じ理屈で学習することで、性能アップも理論的には可能であると思います。ただし、高々数パーセントなので、アルゴリズムや、アーキテクチャ変更による効果には、及ばないということだろうと思います。
しかし、AI学習よる成果を何らかの式に落とし込めるということは、AIモデリングの一歩になる可能性があります。ちょうどGPUも購入したので、ソースが公開されたら試してみようかと思います。
Q.週休は、任意の1週間区間で見た場合、必ず1回以上含まれる必要があります。どのように記述したらよいでしょう？
Ans.
貴職場の場合、別に6連勤務禁止、という制約があります。この制約は、上記より上位の制約になります。任意の1週間区間で見た場合、必ず1回以上含まれる⇒7日週休無は禁止ということです。6連続週休無禁止は、7日週休無禁止を必ず含みます。よって、6連続週休禁止とすれば十分です。
2行目の記述は、このパターンに対する特殊ケースの記述です。入り後は、必ず明けとなることに注意します。制約最終日に入りが来た場合は、翌月1日は、必ず明けとなるので、連続週休無4日で切らないといけないことに注意してください。
Ans. この職場では、規定があり、日曜日休みを１回以上入れることはハード制約となっています。（通常は、実現が難しいと思われますので、ソフト制約とするのが常道です。）
なお、出来れば２回という意味で、２回以上は、ソフト制約にしています。
Ans.遅番・長日パターンを禁止すればOKです。
「xxxを不可」という場合には、単純のその「ｘｘｘパターン」を禁止にするだけでよいです。
反対に、「入りの後は明け」 のように、禁止ではなく望ましいパターンの場合の記述は、一般に、
「入りの後明けは禁止」
「明けの前に入りは禁止」
と、両方向から禁止制約にする必要があります。
今回は、禁止なので、そのパターンだけでOKです。
いずれにせよ、上手く動作しているかどうか、予定に書いてみて、あらゆる可能性を考慮したテストパターンを書きます。
そうして、意図通りにエラーが付いているのを見て、初めて検証が完了します。制約を最初から書く場合は、一つ一つ、ステップバイステップで、きちんと動く部品を積み上げていくこと姿勢が肝要となります。
Ans.
■予定制約レベル１は、予定をソフト制約化した覚えがなくても出現することがあります。
■出現の可能性があるのは、下記オプションをチェックし、かつ先月部で、スタッフ毎のシフト設定等のハード制約と、予定との矛盾の可能性があるときです。その場合、GUIが自動でそのセルをソフト制約レベル１にソフト制約化します。
■スタッフ毎のシフトは、ハード制約です。一方、先月予定もハード制約が普通なので、先月予定部が矛盾が起こり「解がない」事態となることがあり得ます。これを回避するオプションをチェックしたときに、起こり得ます。
■矛盾が無ければ、選択してハード制約化してもOKです。
An Efficient Local Search Solver for Mixed Integer Programming
を見ると、これは凄いなと思ってやってみました。
しかし、スケジュールナースと比べるべくもありませんでした。
確かにこの発想は、今までになかったものです。Gurobiが速いのは、Heuristicsが速いからだ、という噂もある位で、有効なUB解を早く見つけるのは、MIP解法においても有効です。Feasibleな解を早く見つけるのには、有効ですが、厳密解に近いところを見つけるのは、苦手のようです。MIPはリニアソルバが鍵となっており、そこと絡めないと厳密解に近いところは、原理的に難しいのでは？と思います。リニアソルバと平面削除法は、長い長い歴史の積み重ねがあるので、ここに立ち向かうのは勇気があります。ニッチの分野になるかもしれませんが、知見を積み重ねて改善されることを期待したいと思います。
INRC2の難問インスタンスの内の一つの最適値が確定しました。これでOpen Instancesは、残り３となりました。
n100w8_0_0-1-7-8-9-1-5-4 LB:2030 UB:2030
です。
これを、解くのに4カ月かかってしまいました。これの何が難しいかというと、最適値である証明です。UB:2030は、比較的容易に得られますが、他にこれ以上良い解はこの世に存在しない、というのが大変難しいです。通常のBranch＆Boundでは、100万秒走らせたとしても証明は得られません。初期LB-UB Gapは、１０以下であり、容易なように見えますが、実は難問中の難問です。
このインスタンスを解く努力を積み重ねることで、多くのことを学習し、また知見を得ました。で、このインスタンスで特徴的なのは、gap narrowing gain（私の造語）が極めて低いことにあります。その原因としては、構造的なsymmetryがあると思います。これを打ち破る方法としてsymmetry breakingがありますが、その方法については、また別な機会に。
Ans.
では、単純な包含関係にあったので、制約追加で上手く行きました。
しかし、今回は、包含関係にないので、単純な制約追加では上手く行きません。
変更前記述は次のようになっています。
よく間違える記述の例です。
不等式制約では、「今月」をDay集合とすることが多いです。制約中の「今月」の定義を見るには、マウスMiddleボタン（ホイールボタン）をクリックすると出てきます。
ちゃんと、今月になっていることが分かります。
下の例では、6連続勤務禁止のパターンで、先月部26日からの5日間が、正しく動くためには必要ですが、先月部2日間のみとなっており、指定を間違えていることが分かります。
Ans.
固定した勤務で、平日のみに出勤することが決まっているならば、スタッフに入れない方がよいです。スケジュールナースは、決まっていないシフトを割り当てるソフトです。
ただし、その方が、カウント対象（例えば日勤者等）であるならば、入れる必要があります。ただし、その方を除外してカウントしてもよいときは、除外カウントして、やはり入れない方がよいです。
対象は出来る限り少なくした方が、求解速度は上がるので、上記目的外のスタッフは、下のようにチェックを外すか、行削除して、当該プロジェクトの対象スタッフではなくします。
Ans. 制約名は、何であってもよいです。スタッフ名である必要はなく、例えば、AとBとかでもOKです。他の制約と区別できることが唯一の条件です。
ですのでユニークな名前にしてください。
例
＜ペア制約について＞
現在、上記のように固有名を用いて記述は可能ですが、記述することは推奨しておりません。退職等でスタッフがいなくなるとエラーとなるためです。
GitHUBの挙げている例の通り、
スタッフプロパティシートは毎月メンテすると思いますので、忘れることは少ないと思います。
Ans.
マイクロソフトアカウントにログインして、
サブスクを停止してください。来月から課金されなくなります。
https://www.nurse-scheduling-software.com/japanese/service/pausing_subscription/
ご利用ありがとうございました。
Q.下図、宿日直回数と休日拘束数とで、医師間のばらつきがいつもより大きいような気がします。何故でしょう？
Ans. １２月勤務表では、１月年始も取り込んで作成している影響だと思います。（物理的要因です。）
試しに、制約最終日を１２月３１日に変更してみました。
上図をよく見比べると、医師間のバラつきは、
制約最終日 宿日直数 休日拘束数
１月５日版 2－４ 4－6
１2月31日版 0－2 2－4
となっており、バラつき（偏差＝２）で変わっていません。全体が多くなっている傾向になっているだけ、ということです。これは、制約日数が5日だけ増えている影響とみることが出来ます。
この勤務表のスタッフプロパティシートは、制約区間全体に効いてくるので、適宜最適値に調整してください。
変更前
また偏差も2以下に収まっています。
休日の丸1日の宿日直、あるいは休日拘束1回に対してカウントは、２です。つまり、回数に直すと1回の偏差となります。この1回の偏差は物理制約による限界です。全員が偏差0とするには、
Σ宿日直％医師数==0
になる必要があります。平たく言うと、端数が0になる必要があります。逆に言えば、全員が偏差0となるには、端数0となるときだけです。
例えば、宿日直コマ数総和40に対して、医師が10人いれば、全員4回で均等にできますが、41の場合は、割り切れず、必ず偏差が１となります。5回行う方が1人だけ生じます。
つまり、1回の偏差が生じるのは物理限界であって、なんら不思議ではありません。
大変、参考になる論文が出ました。
PDLPは、諦めていたのですが、GPU実装を使えば、可能性があることが示されています。最近のGurobiもGPUを使い始めたのは知りませんでした。
Simplex、内点法、FirstOrderの比較考証もされています。Simplexのマルチスレッド化は、LU分解のパラレル化が困難でした。Julian Hall教授の実装もありますが、CPUキャッシュに収まりきれないと性能が出ない問題があります。また、従来IPMにしてもスパースコルスキー分解を上手くGPUに載せるのは、難しいと考えられてきました。
ここにきて、FirstOrderは、激しく性能向上争いが続いていて、ADMMを用いた方法も注目しています。
以上のトレンドを鑑みて、GPUによる実装を検討してみようと思います。（あくまで記録更新用なので、一般の実装には影響しません。ABIP+にせよPDLPにせよ、ユーザにとっては、精度と速度が出れば何でもよいです。）
＜Simplexは必要ないか？＞
依然として必要です。なぜなら、HotStart（WarmStart）によく駆動は、Simplexによるからです。INRC2規模では、Simplexのhoststartによる方が速いのでSimplexは欠かせません。一方、超大規模、SchedulingBenchmarksのInstance23/24規模になると、SimplexはHotstartを使っても無力です。この場合、内点法かFirstOrderによる方法となります。（FirstOrderによるHotStartは、Starandmarkさんの論文にあるのですが、大して効果がなかったような印象が残っています。）
上記論文で使われているGPUは、とんでもなく高価なものですが、上のような背景の私の用途としては、普通の世代落ちしたもので十分効果があるだろう、と見ています。
CUDAが使えるＧＰＵは、以下のページで分かります。
CUDA GPUs - Compute Capability | NVIDIA Developer
とりあえず、GPUを購入して勉強・評価して、COPTを使用するかどうかを判断したいと思います。
AIの流行により、一気に花開いたGPUですが、アークテクチャを見ると、ハードウェアとソフトウェア（コンパイラ技術）の見事なバランス感覚で成り立っており、両分野に精通した人の設計なんだろうな、と思います。CPUでマルチスレッドにするとキャッシュメモリがボトルネックとなり、その部分を分離できるという意味においても一時の流行に終わることがなく、今後も汎用化が加速していくのでないかと推測します。
今まで、ユーザさまのPCにローカルファイルで保存することを推奨してきたのですが、その選択がなくなり、勝手にクラウドに録画される仕様に変更になったみたいです。
で、この録画、AI要約があったり、文字起こしがあったりで、再度見たい箇所を素早く探すことが出来るようです。ダウンロードではなく、パスコードリンクを送ることで、ユーザさまも文字起こし付のサイトで視聴できる、ということのようです。
AI要約は、次のレベルでまだまだ、です。
次は、昨日行ったAI要約です。
--
ミーティング後、ユーザさまにパスコード付きのリンクを私菅原氏とｘｘ氏は、クラウドレコーディングシステムの導入やスタッフの休暇管理、システムにおける制約の重要性について話し合いました。 また、スケジュール変更のプロセス、ソフトウェア制約の使用、スタッフ定義を設定し、過剰と不足を調整することの重要性にも焦点が当てられました。 会話は、新しいシステムの実装、複雑な制約に対応できるシステムの必要性、ソフトウェア制約を維持することの重要性について議論で終わりましたが送れば、ユーザさまの視聴が可能です。
菅原さんとｘｘさんは、Excelの使い方をｘｘさんに教えることに焦点を当てた4時間のセッションを行い、菅原さんが指導や制限事項を提供しました。 セッションは、菅原が後でｘｘにファイルを送ることを約束して終了しました。 両参加者は、このセッションに感謝の意を表しました。
--
プロジェクトファイルが、全く動かない状態からのスタートでした。なので、制約を一から作りこむレクチャを行いました。
■仕様の聞き取り・確認
■頂いたプロジェクトファイルをベースにしながら、一から制約を作りこんでいきました。
■特に留意する点、注意事項など、その都度、質問を受けながら
■全ての実装したい制約を実装
し、その場で、ブランク予定でエラー０まで実装確認を行いました。
知人からの紹介とのことで、「知人のプロジェクトファイルをベースに、サブスクをご契約頂いて著書も購入したけれでも、全くどうすればよいか分からない」
とのことでしたが、出来栄えにご納得頂けたと思います。気づけば４時間程経っていました。OJTで、なおかつプロジェクトファイルが出来上がりました。
勿論、ご自分で一から練習してみるのが最も大事、というお話しはさせていただきました。４時間分の録画はあるので、見たいところや聞き逃したところ等、見返すことが出来、これと併せて、その職場にマッチした最適な学習教材（当該プロジェクトの解説資料５０ページ添付）にもなったと思います。
が、これほど短時間に実装できるスケジュールナースは、
凄いな！スケジュールナース！
と改めて思った次第です。慣れれば最強は疑うところなし、です。
先生には、RAMP発表の折にお世話になっていて、ORの学術世界を垣間見ることが出来ました。著書も購入しています。
Amazon.co.jp: IT Text 数理最適化 : 久野 誉人, 繁野 麻衣子, 後藤 順哉: 本
この本は、分岐限定法と妥当不等式について解説している殆ど唯一の日本語本だと思います。
ふと巻頭言を見る機会がありました。
-数 理 の 専 門家で ない 人 が ， 対象 を的確 に捉 え，必要 な とこ ろを抽象化 してモ デル を作成する こ とが で きれ ば， コ ン ピ ュ ー タの 性能が一段 と向上 してい る現在で は ， 我 々 の 研 究成果 が応用 され る機会が増す と考え る．誰 もが モ デ リン グの技術を身 に つ け るた め に は ， ど うすれ ば よい か 欲を言 え ぱ ， 数理 的な思 考 をと しない 人 に も対象を整 理 して モ デ リン グの 方向性が わか る よ うなそ ん な指針 を構築 したいと常 日頃考えて い る．
これは、私が常々、感じ考えていることと全く同じであります。ソフトの使い方以前に、考えを整理する術が必要です。
最近ZOOMレクチャを意図的に多くしています。（メール回答で終わらずにZOOMで解説）分からないことが分からない自分にとって、有益な機会であることが多いです。
1年のサポート中、大体が3回程度以下で済みます。プロジェクト作成で、私が生み出したバグもあるし、お客さまの仕様変更もあるし、ですが、その後は、殆どサポートしなくとも運用出来ているようです。
今回は、実装その３です。
１）制約終了日を１月５日する
２）１２月の公休区間を作成する
従来の「今月」は、制約終了日を年始１月５日としたために、１２月１日ー１月５日が「今月」扱いになってしまいます。このため、公休数区間は、１２月１日－12月３１日となるように新たに定義します。
３）公休数を制約しているところを「今月」⇒「今月区間」に置き換えてやります。
４）スタッフプロパティシートを調整する
夜勤数は、年始まで含んだ夜勤数になるので、普段より多めに設定する必要があります。
公休数については、普段通り、１２月の公休数を入力します。
５）オプション
以上が基本の枠ですが、多分、年始の各スタッフの夜勤数については制約する必要があるでしょう。
次のその実装例です。
次は、マクロで行う例です。
一長一短です。このほかに、出てきた解を予定で調整してしまうのもアリだと思います。
どれを使ってもOKです。自分が分かり易い方法が一番です。
以上３回に渡って年末年始の実装を解説しました。
今回は、実装２です。
この方式は、特殊です。スケジュールナースの実装というよりは、クジの作り方のようなお話です。
前提条件として、以下のような職場の仕様です。
１）年末年始区間が定められており、その期間にｘ回以上の公休を取るように事務局から通達がある。
２）年末年始を除いた公休数は事務局より通達があり定められている。
３）年末年始区間の希望は取らない（取れない）完全にクジで決まる。
え、希望は出せないの？と思うかもしれませが、それについては後述します。
で、クジの作り方です。以下は、クジの説明図です。
勤務するスタッフA-Pまでクジを作ります。クジには、年末年始区間の勤務パターン記されています。このパターンは１）要求も満たすようにつくられています。それを引いたスタッフはそのクジのパターン通りに働かなければなりません。希望があって、働けない場合は、同じスキルレベルのスタッフ間でやり取りして調整することになっています。
このクジは、必要な夜勤数や日勤数が必ず揃うようになっています。（完成した全体パターンをハサミで切り取ってクジにしています）
クジによって、年末年始区間の勤務は完全に決定します。これを１２月・１月の勤務表各々において、予定として取り込めばよい、ということになります。
完全に神様任せでありながら、組織や事務局の要求を完全に満たすという優れた方式だと思います。これなら文句を言われることがありません。「希望不可」という一見トリッキーでありながら、誰からも文句を言われない素晴らしい方法ではないかと思います。
で、この場合、クジで決まった予定をスケジュールナースに入力することでよいので、年末年始に関わる制約を記述する必要はありません。唯一、年末年始を除いたところの公休数は、12月と1月が通常から変わるので、その部分だけ制約を追加する必要があります。
これは以下のように記述しておくとメンテナンスフリーに出来ます。
「特別の日の設定」年末年始を年間カレンダで設定します。
以上です。
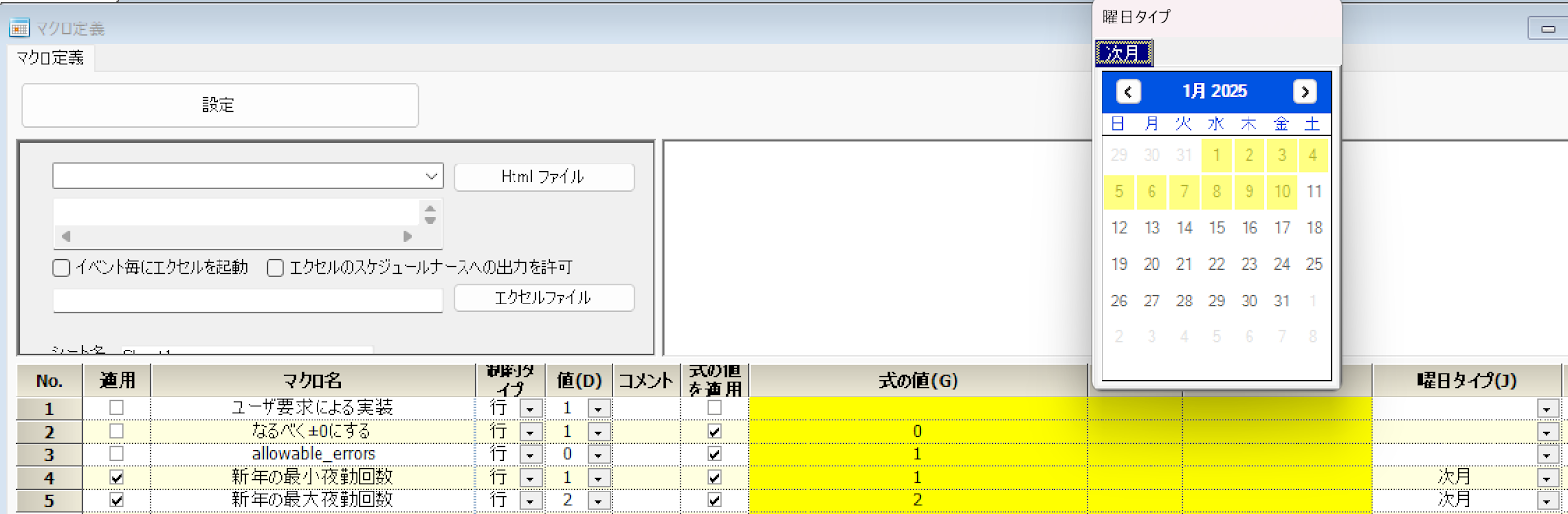
年末年始がやってきました。
そこで、スケジュールナースでの、年末年始の実装をまとめてみたいと思います。年末年始の実装方法としては、3種類あります。
１）通常のプロジェクトファイルを変更せずに、１２月と１月の勤務を各々別につくる（普段のプロジェクトと変わらないが年始希望を考慮して予定を組み込む）
２）年末年始区間は、くじ方式。年末年始外の公休数を別に制約
３）年末月は、年始の希望を含んで制約する
以上の3つです。
早速、第一の方法を説明します。
１）通常のプロジェクトファイルを変更せずに、１２月と１月の勤務を各々別につくる（普段のプロジェクトと変わらないが年始希望を考慮して予定を組み込む）
この場合、特に年末年始に特別な制約を加えることはなく、普段通りに作ります。１２月勤務表を作ったあと直ぐに１月勤務表も作ります。ただし１月勤務表で実際に採用するのは、年始区間のみです。
１）１２月の勤務表を完成させる。決定した解を１月勤務表では予定に送ります。
Ans.新人は、夜勤者数にカウントしないので、1回だけ異動者は夜勤者数にカウントしなければよい、ということになります。この実装としては、既に、
「新人初回夜勤区間は、新人を含めないで通常夜勤者数を確保したい」
であります。この例と同じようにすればよいですが、今回は、マクロを使わないで実装してみます。
