最適である証明

「最適」であることの証明は、どのようにすればよいでしょうか？　現在の解が最適であることを証明するには、現在の解よりも良い解が存在しないことを証明しなければなりません。存在しないことの証明はどうすればよいのでしょうか？

私の知る限りにおいて二つの方法しかありません。今日は、その方法のうちの一つをお話します。

＜数理ソルバによる方法＞

緩和化された問題を解いて、それよりも下回る解がないことを証明する方法です。緩和化とは、問題の条件を緩くすることで、具体的には、離散化した系を連続系にしてしまいます。連続系だと、Simplexなりバリアソルバ等の連続系ソルバがあります。これを用いれば、連続系の最適値は、求まります。（条件の緩やかな、連続系の目的関数値が求まります。）で、組み合わせ最適化の解は、不連続な離散系の解ですが、緩やかな連続系の値よりも、良い値であるはずがない、という風に考えます。つまり目的関数値の下限が、求まります。

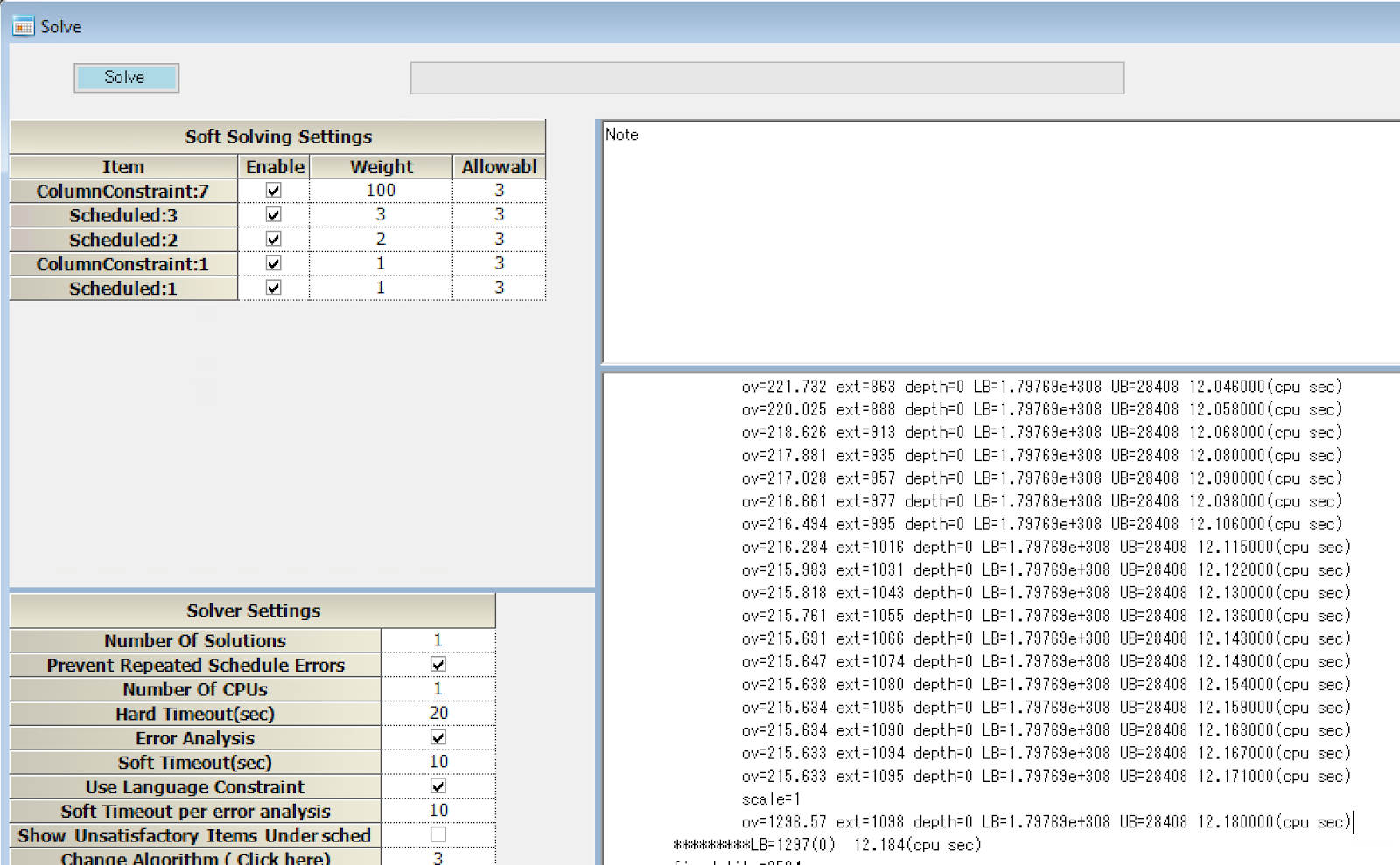
例としてScheduling Benchmarks　Instance8は、スケジュールナースだと次のような感じです。

LB＝1297というのが、LowerBoundを表しています。これが連続系の値で、ここまで12秒かかっています。この解は、連続系の解であって、離散系、すなわち、組み合わせ最適化の系ではないので、実用には寄与しません。ただし、連続系で1297だから、本当の系では、運がよければ、この値か、これより大きい値になるはずだ、ということは分かります。つまりこの段階で、目的関数値は、1297未満には絶対に行くことはない、ということが分かります。ここまで12秒です。

実際の系では、このあとアルゴリズム１で、整数化を行っています。

最初のトライで、UB=1403 まで来ています。これはBranchingTree　Rootでの整数解で実用的です。本当の目的関数値は、

LB=1297<=最適目的関数値<=1403

のどこかにある訳です。其のあとに行う作業は、Branch＆Boundです。

時々整数化を実施しながら、Branching Treeを下がっていきます。Depth14で、1398となりました。

本当の目的関数値は、

LB=1297<=最適目的関数値<=1398 

にあります。

さらに、

本当の目的関数値は、

LB=1297<=最適目的関数値<=1304

にあります。段々狭まってきました。 

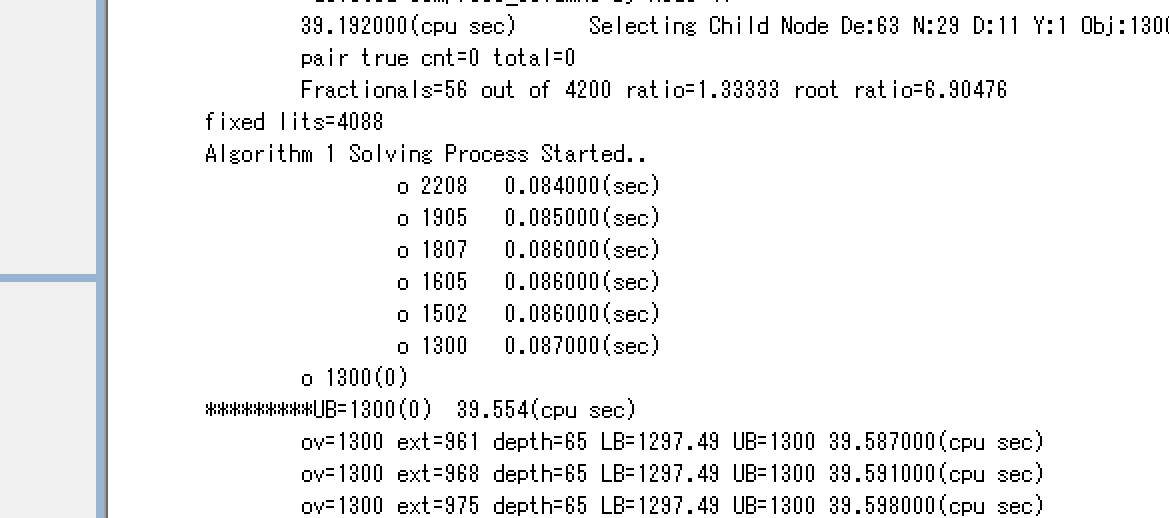
にあります。さらに、Depth64で、

LB=1297<=最適目的関数値<=1300 

となりました。これから後のTreeは、Branchingして1300以上ならそれ以上は見る必要はないので、枝刈りすることできます。こうして、全てのTreeを見て、1300未満以下の整数解は存在しないという証明ができるまで、Treeを網羅することになります。

スケジュールナースでは、この証明を62秒で出来ており、2位（Gurobi）を5倍以上、3位（CPLEX）を10倍以上離して世界最速です。

数理ソルバによる方法は、このように連続系を用いるのが鍵となっており、CuttingPlaneや整数化ヒューリスティック等、数理学的アプローチにより解を求めています。

実務では、こんなに綺麗に行くことはまれでとくに、ペア制約があるとまず収束しません。この部分が今行おうとしている改善事項になります。また、現状ソフト不等式が多いと、スピード劣化が顕著にあります。この点についてもRCSPP改善計画で報告どおり改善予定です。10－100倍程度の高速化を予定しています。これによりScheduling Benchmarksのみならず全てのインスタンスにおいて圧倒的な高速と高精度を実現する予定です。