2020年4月30日木曜日

AWSの環境整備

次の事項を行いました。

■Amazon　アカウントの取得
■ルートアカウントの2段階認証　（Google　Authentification使用）

■WSL　Ubuntu20.04　インストール　（Microsoft Storeより）
■VisualC++2019　インストール
■aws cli のインストール
■nano editorのインストール
　viは、無理..


Amazon は、当然Linux環境になるので、コンパイラは、g++か、clangになるのですが、最近、VisualC++でも、WSL上で、直接にデバグ出来るようなったようなので、VisualC++2019でやってみようと思いました。

当面、AWS上で、サンプルをいじりながら、理解して行こうと思います。この歳で新しい技術を学ぶことになるとは思っていませんでしたが、鞭打って頑張ってみようと思います。






投稿者 時刻: 0 件のコメント:

2020年4月29日水曜日

AWS の構成

上が構成図になります。WebSocketで接続して、スケジューリング問題をJSON形式で受け取り、
求解状況と、最終的な解を送出します。以前、VPSで同じ構成で試したことがありますが、それをサーバレスのクラウド化を行うという、文字通りソルバーのクラウド化です。GUIは、持ちません。エンジンのみです。

AWS化の課題は、色々ありますが、一番は、私はAWSについては、初めてで良く分かっていないことです。加えて、C++のLambdaは、参考になる事例がほとんどなく、WEBSocket構成でできるのかどうかも良く判りません。なので、その辺のFeasiblityStudyを行いつつ、構成を一つ一つ組み上げていくことから始まります。
投稿者 時刻: 0 件のコメント:

2020年4月28日火曜日

今後の計画


■SC3正式版リリース　5月End
　Algorithm1のみのサポートとなります。SC3用のマニュアルを作ること、及びビデオチュートリアルの追加を予定しています。SC２は保守扱いとします。また、Algorithm0は、削除する予定です。
　
■Cloud版エンジンの開発設計　6-12月
　AWSによるCloundエンジンの開発を行います。
　
■Microsoft　Store版　Desktop　
　優先度としては、一番低くなってしまいますが、適宜開発を進めていきたいと思います。
　
投稿者 時刻: 0 件のコメント:

2020年4月27日月曜日

オレゴン州の状況

１０年以上顧客で、今も時々メールをくださるジョンさんに教えて頂きました。この後、our presidenｔ..があるのですが、それは、割愛。

Oregon has a "mild" lock-down" with restaurants, bars, and other social gathering
places closed. Many churches have closed and are doing online services. A lot
of companies are doing mostly "work-from-home" and video conferencing. The
governor is looking at statistics to see when it will be OK to start easing off
restrictions.
As for us, since we live in a suburb that is not very crowded, we go out for walks
and try to enjoy the flowering trees and gardens. We carefully go out shopping
once a week and stores are asking people to stay 2 meters apart.

Stay well!
投稿者 時刻: 0 件のコメント:

Instance20の新解が発見されてしまった

既に私が発見していたInstance20の新解が報告されてしまいました。4769は、既報通りで、正しい値です。

ぐずぐずしているからですね。Paperが準備中らしいので、興味深く、楽しみです。残されたインスタンスで未知で、未だ厳密解が報告されていないのは、Instance15/21/22..になってしまいました。Instance15は、報告していない新解を持っていますが、これが唯一となってしまいました。

Instance21/22については、線形ソルバーの高速化が必須で、私のところでも、厳密解に近いところを求めようとすると現状100日位かかってしまいます。

Instance23/24については、規模オーダが一桁違うので、Petter Strandmarkさんの手法か、メタヒューリスティクス等、別なアプローチが要ります。この辺は、数理ソルバーは、勿論、SATでも限界を超えていると思います。INRC2のようなダイナミックスケジューリングが、現実的アプローチになるのではないでしょうか？

投稿者 時刻: 0 件のコメント:

2020年4月26日日曜日

SAT2020延期か

今年は、イタリアでの開催予定ですが、リモートにするか延期するか未だ悩んでいるようです。
人口知能学会もリモートの視聴の案内が着ましたし、今年だけなのか、今年からなのか、イベントの開催要項も様変わりするのかもしれません。
投稿者 時刻: 0 件のコメント:

2020年4月25日土曜日

129Aをリリースしました

エンジンを少しいじりました。大規模インスタンスに対して動作を少し変えていて、ソフトレベルが多くなっても大丈夫だと思います。他に、本来エラーを出すべきところが漏れていたところがあったので、修正しています。

前回報告したように、Algorithm4は,学術ベンチマークについては、StateOfArt数理ソルバーを凌駕し、無類の強さを発揮しますが、実務インスタンスでは、コンパイルすら通らないのが多いのは変わっていません。この原因については、追って説明したいと思います。
投稿者 時刻: 0 件のコメント:

2020年4月24日金曜日

特許化検討

ソフトウェア特許の場合、特に何らかの解法に関する特許関し、他者がそれをライセンスを受けずに実施していることを発見するのは、難しいと思います。表示に関するものでしたら侵害の発見は容易ですが、計算方法の類では、まず難しいと思います。　それ故に、内部に留めたほうが良いこともあります。ですが、私の場合、アプリの販売もありますが、ソルバーとして使って頂いているお客さまもあり、製品性能がトップであることをアピールする重要なツールでもあります。特許権の維持には、コストがかかるのですが、それに見合うだけの価値がある、と勝手に判断した場合には、特許化することにしています。

特許化の最も大きな障害は、審査官とのやり取りです。ほぼ100%拒絶通知が来ます。その拒絶理由について、一つ一つ反論をしないといけないのですが、これがとてつもなく面倒です。およそ現代の特許で、ある技術とある技術の組み合わせではない特許はほぼないと言っても過言ではないと思いますが、審査官は、そこを突いてきます。で、よくあるのが、クレームの一つの文言だけが一致する、先願または、引用文献を示してきます。一つ一つは、全く関係のない技術なのですが、必殺の「...してみれば、引用文献を用いて、本願発明とすることは、当事業者が容易になしえた事項である。」で、片付けられてしまいます。内容を理解もされずに、進歩性云々の要件で却下されることが多いと思います。

これを防ぐ手段を考えてました。有効なのは、コンペティション優勝、または世界記録を更新した、ということです。もし、容易になしえる技術ならば、優勝は自分ではなく、世界記録は、既に誰かが更新しているでしょう。本願を用いて世界記録を更新した、ということであれば、「容易になしえる技術」に、明確に反論することが出来るでしょう。

ベンチマークの目的関数値の更新に固執している理由は、こんな背景もあります。
投稿者 時刻: 0 件のコメント:

2020年4月23日木曜日

ログ整形スクリプト

NEOS-ServerのGurobiデータとSC3のデータを拾うスクリプトを書きました。
下がGurobi用です。
import re
import csv
f = open('120w4gurobi.txt', 'r')
line = f.readline()
mode=0
map={ }
read_enable=False
constant=1480 #Constant objective value
while line:
 #print(line.strip())
 if 'Gap' in line:
  read_enable=True
 if 'ERROR' in line:
  read_enable=False
 if read_enable:
  print(line)
  l = line.split()
  count=0;
  second=''
  for s in reversed(l):
  
   if count==0 and 's' in s:
    second=s.replace('s','')
    print(second)
   if count==4:
    print(s)
    if second !='':
     map[int(second)]=float(s)+constant
   count+=1
 line = f.readline()
f.close()
#print(map)
map=sorted(map.items())
print(map)
f = open('result.csv', 'w')

for s in map:
 print(s[0])
 s1=str(s[0])+','+str(s[1])
 s1+='\n'
 f.write(s1) 
f.close()
 
SC3用が下です。
import re
import csv
f = open('result.txt', 'r')
line = f.readline()
mode=0
map={ }
read_enable=False
constant_time=213.809 #Algorithm1 Solving Process Started time
once=False
while line:
 #print(line.strip())
 if 'Algorithm 1 Solving Process Started.' in line and once==False:
  read_enable=True
  once=True
 if '*********UB=' in line:
  read_enable=False
 if read_enable:
  #print(line)
  l = line.split()
  count=0;
  second=''
  for s in reversed(l):
  
   if count==0 and '(sec)' in s:
    second=s.replace('(sec)','')
    print(second)
   if count==1:
    print(s)
    if second !='':
     sec=float(second)+constant_time
     map[sec]=float(s)
   count+=1
 line = f.readline()
f.close()
#print(map)
map=sorted(map.items())
print(map)
f = open('result.csv', 'w')

for s in map:
 print(s[0])
 s1=str(s[0])+','+str(s[1])
 s1+='\n'
 f.write(s1) 
f.close()
 
で、グラフが下です。
これだと、良く判らないので、横（時間）、縦（目的関数値）で拡大してみます。
さらに縦を拡大します。
グラフから、■Algorithm1は、計測直後から実行可能解が出力されます。遅れて、Algorithm4は、200秒、Gurobiは、767sec後から実行可能解が出力されます。
■Algorithm4は、330secで打ち切っていますが、それでも8時間後のGurobiよりも良い目的関数値になっています。

ナーススケジューリング解の設計目標として、良い解を出来る限り早く出力すること、がありますが、どちらかというと学術分野では、速さよりも時間をかけたときの目的関数値の優劣を競う面があります。その意味で、Algorithm4が、最終的な目的関数値が最小ですので優秀なのですが、実務的には、

■数分内に実用的な目的関数値を出力する

ことの方がより重要です。仮に8時間後に厳密解が判ったとしても、その差が数%内ならば、数分内に出力される方を選ぶでしょう。なぜならナーススケジューリングは、一回で解を得ておしまいではなく、何回もの試行を経て決定されることが一般的だからです。その意味で、解の有無が直ぐに判るAlgorithm1が最も実務的です。

が、ソフトエラーが多数に渡る場合、GAP（下界と上界の差）が、今回のように50%程度になることもあります。そのAlgorith1のこうした弱点を補うことが今回のAlgorithm4の目的でした。狙い通り、
INRCⅡの殆ど全てのインスタンス及びSchedulingBenchmarkのBestKnown値の更新、いくつかの成果はありました。残念ながら、実用的には、今だ道が遠いのですが、作業予定時間を大幅に超過してしまいました。これまでの成果をまとめて一区切りとしたいと思います。

■厳密解が確定
その後、テストを続けた結果厳密解が確定しました。16000sec後にAlgorithm4が確定(2050）させました。120W4というのは、スタッフ120人のWeeksが4です。確定できたのは、僅か数インスタンスしかないのですが、必ずしもインスタンス的に小さいものでないことが興味深いです。




投稿者 時刻: 0 件のコメント:

2020年4月22日水曜日

NEOS SERVER LOG

下は、CPLEXのログになりますが、Elapsed　Timeが表示されるまで、時間の経緯が判りません。
これでは、時間ー目的関数値　の推移グラフが書けません。


        Nodes                                         Cuts/
   Node  Left     Objective  IInf  Best Integer    Best Bound    ItCnt     Gap
*     0+    0                       359195.0000     -370.0000           100.10%
      0     0      -64.2187  3315   359195.0000      -64.2187       19  100.02%
*     0+    0                        43470.0000      -64.2187           100.15%
      0     0       53.7500  2331    43470.0000     Cuts: 279    18717   99.88%
      0     0      110.7778  2628    43470.0000     Cuts: 759    27889   99.75%
      0     0      148.0682  2551    43470.0000     Cuts: 703    38963   99.66%
*     0+    0                        29975.0000      148.0682            99.51%
*     0+    0                        29915.0000      148.0682            99.51%
*     0+    0                        29905.0000      148.0682            99.50%
*     0+    0                        29705.0000      148.0682            99.50%
*     0+    0                        28675.0000      148.0682            99.48%
      0     0      178.1077  2688    28675.0000     Cuts: 729    48298   99.38%
      0     0      216.1885  2671    28675.0000     Cuts: 677    64088   99.25%
      0     0      242.7695  2696    28675.0000     Cuts: 647    72639   99.15%
      0     0      253.8045  2680    28675.0000     Cuts: 623    81504   99.11%
      0     0      270.4266  2508    28675.0000     Cuts: 662    90893   99.06%
      0     0      277.8454  2682    28675.0000     Cuts: 569   101580   99.03%
      0     0      288.5256  2773    28675.0000     Cuts: 570   112909   98.99%
      0     0      294.7174  2735    28675.0000     Cuts: 654   125075   98.97%
      0     0      307.0973  2715    28675.0000     Cuts: 574   134680   98.93%
      0     0      313.8889  2563    28675.0000     Cuts: 569   144764   98.91%
      0     0      318.3333  2735    28675.0000     Cuts: 501   154305   98.89%
      0     0      320.6537  2686    28675.0000     Cuts: 428   165201   98.88%
      0     0      324.8424  2511    28675.0000     Cuts: 479   176102   98.87%
      0     0      328.7166  2701    28675.0000     Cuts: 486   186932   98.85%
      0     0      331.1991  2640    28675.0000     Cuts: 467   196434   98.84%
      0     0      333.7144  2667    28675.0000     Cuts: 511   206362   98.84%
      0     0      335.4018  2422    28675.0000     Cuts: 452   214946   98.83%
*     0+    0                        13650.0000      335.4018            97.54%
      0     0      337.7659  2424    13650.0000     Cuts: 446   224872   97.53%
*     0+    0                         4360.0000      337.7659            92.25%
*     0+    0                         4210.0000      337.7659            91.98%
*     0+    0                         4180.0000      337.7659            91.92%
*     0+    0                         4130.0000      337.7659            91.82%
*     0+    0                         4120.0000      337.7659            91.80%
*     0+    0                         4105.0000      337.7659            91.77%
*     0+    0                         4095.0000      337.7659            91.75%
*     0+    0                         4080.0000      337.7659            91.72%
*     0+    0                         4065.0000      337.7659            91.69%
*     0+    0                         2315.0000      337.7659            85.41%
*     0+    0                         2100.0000      337.7659            83.92%
*     0+    0                         2085.0000      337.7659            83.80%
*     0+    0                         2075.0000      337.7659            83.72%
*     0+    0                         2065.0000      337.7659            83.64%
*     0+    0                         2055.0000      337.7659            83.56%
*     0+    0                         1985.0000      337.7659            82.98%
      0     0      338.7064  2534     1985.0000     Cuts: 341   233655   82.94%
      0     0      338.9290  2501     1985.0000     Cuts: 449   243012   82.93%
      0     0      340.3071  2604     1985.0000     Cuts: 400   252547   82.86%
      0     0      342.6351  2680     1985.0000     Cuts: 479   262409   82.74%
      0     0      345.2399  2705     1985.0000     Cuts: 468   271762   82.61%
      0     0      346.5593  2594     1985.0000     Cuts: 392   281214   82.54%
      0     0      348.2926  2696     1985.0000     Cuts: 424   291728   82.45%
      0     0      348.6862  2780     1985.0000     Cuts: 400   301858   82.43%
      0     0      352.1631  2469     1985.0000     Cuts: 466   311631   82.26%
      0     0      353.1727  2388     1985.0000     Cuts: 518   322374   82.21%
      0     0      354.3967  2365     1985.0000     Cuts: 402   333125   82.15%
      0     0      356.1600  2490     1985.0000     Cuts: 409   344215   82.06%
*     0+    0                         1785.0000      356.1600            80.05%
      0     0      356.3396  2468     1785.0000     Cuts: 458   354575   80.04%
      0     0      358.8643  2531     1785.0000     Cuts: 340   365518   79.90%
      0     0      359.0449  2455     1785.0000     Cuts: 499   380153   79.89%
      0     0      359.3243  2318     1785.0000     Cuts: 395   410059   79.87%
      0     0      360.6046  2354     1785.0000     Cuts: 463   424344   79.80%
      0     0      361.3983  2513     1785.0000     Cuts: 445   438669   79.75%
      0     0      363.0090  2273     1785.0000     Cuts: 429   450682   79.66%
      0     0      364.2676  2379     1785.0000     Cuts: 453   460801   79.59%
      0     0      364.5254  2297     1785.0000     Cuts: 453   473808   79.58%
      0     0      366.6675  2711     1785.0000     Cuts: 363   487309   79.46%
      0     0      369.5115  2678     1785.0000     Cuts: 440   501845   79.30%
      0     0      369.6678  2527     1785.0000     Cuts: 447   515283   79.29%
      0     0      370.5862  2485     1785.0000     Cuts: 409   526362   79.24%
      0     0      372.0121  2644     1785.0000     Cuts: 441   537949   79.16%
      0     0      372.7673  2541     1785.0000     Cuts: 417   561352   79.12%
*     0+    0                         1775.0000      372.7673            79.00%
      0     0      373.3979  2573     1775.0000     Cuts: 443   571316   78.96%
*     0+    0                         1665.0000      373.3979            77.57%
      0     0      374.5699  2491     1665.0000     Cuts: 411   593582   77.50%
      0     0      375.9199  2535     1665.0000     Cuts: 411   606301   77.42%
      0     0      376.9399  2510     1665.0000     Cuts: 427   618234   77.36%
      0     0      377.4003  2617     1665.0000     Cuts: 426   628252   77.33%
      0     0      378.4336  2562     1665.0000     Cuts: 413   641045   77.27%
      0     0      379.1902  2433     1665.0000     Cuts: 404   651619   77.23%
      0     0      381.9274  2640     1665.0000     Cuts: 443   663832   77.06%
      0     0      382.7832  2655     1665.0000     Cuts: 449   688911   77.01%
      0     0      383.8327  2516     1665.0000     Cuts: 478   700613   76.95%
      0     0      384.2792  2581     1665.0000     Cuts: 434   719632   76.92%
      0     0      385.4148  2659     1665.0000     Cuts: 305   731989   76.85%
      0     0      387.5154  2595     1665.0000     Cuts: 457   741474   76.73%
      0     0      390.1512  2554     1665.0000     Cuts: 461   750275   76.57%
      0     0      391.2088  2629     1665.0000     Cuts: 366   759972   76.50%
      0     0      393.4489  2724     1665.0000     Cuts: 597   768781   76.37%
      0     0      394.2833  2650     1665.0000     Cuts: 465   781215   76.32%
      0     0      394.7189  2601     1665.0000     Cuts: 404   790527   76.29%
      0     0      396.0850  2609     1665.0000     Cuts: 483   802531   76.21%
      0     0      396.9782  2520     1665.0000     Cuts: 402   817779   76.16%
      0     0      399.2371  2635     1665.0000     Cuts: 443   829483   76.02%
      0     0      399.7541  2654     1665.0000     Cuts: 401   838973   75.99%
      0     0      400.5069  2506     1665.0000     Cuts: 475   860150   75.95%
      0     0      401.0033  2533     1665.0000     Cuts: 541   870828   75.92%
      0     0      401.1352  2633     1665.0000     Cuts: 441   880720   75.91%
      0     0      401.3362  2377     1665.0000     Cuts: 141   891428   75.90%
      0     0      401.6659  2670     1665.0000     Cuts: 610   903345   75.88%
      0     0      402.2398  2599     1665.0000     Cuts: 353   915823   75.84%
      0     0      402.3160  2585     1665.0000     Cuts: 481   929191   75.84%
Heuristic still looking.
Heuristic still looking.
*     0+    0                         1630.0000      402.3160            75.32%
      0     2      402.3160  2585     1630.0000      402.3160   929191   75.32%
Elapsed time = 10455.15 sec. (1830372.98 ticks, tree = 0.02 MB, solutions = 28)
      1     3      402.3160  2569     1630.0000      402.3160   930957   75.32%
      2     4      402.4682  2570     1630.0000      402.3160   933742   75.32%
      3     5      403.9569  2529     1630.0000      402.3160   936012   75.32%
*     4+    3                         1480.0000      402.3160            72.82%
*     4+    3

一方、GUROBIは、最初にリニアオプティマイザをPrimal・Dual　Simplexにして、Simplexを廻した後、最初の整数解が出るまでに、767secかかっていることがわかります。逐次時間のとともに目的関数値が減少していく様子が判るので、グラフ化できます。同じインスタンスについて、SC3　Algorithm1・Algorithm4　と比較すれば、性能比較の可視化を行うことができます。

それにしても、Feasibleな解がでるまでに10分もかかっていたのでは、使い物になりません。

RAMP講演でも、「CPLEXで解が出なかったインスタンスがある」　と報告して、「おかしいんじゃないか？」という指摘を受けたことがありました。その理由は、NEOS　SERVERのShort Priority(直ぐにやってくれるが5分でタイムアウト）での実行による結果でした。正しくは、「5分で実行可能解が出てこないインスタンスがある。」に訂正します。手持ちお客さまのインスタンスで説明しましたが、
決して特殊な例ではありません。（5分も何も言ってこないのは、解がない　というのが私の感覚でした。）

この例のインスタンスは、INRCⅡの120W4というインスタンスで、規模的には、大きいインスタンスになりますが、超大規模というものではありません。数理的ソルバーの優位性は、厳密解を出せることにありますが、一般のナーススケジューリング問題においては、厳密解を出せるインスタンスというのは、むしろ少ないです。従い実務におけるナーススケジューリング問題では、数理的ソルバーの出番は少なく、主にメタヒューリスティクスによる解法が主になります。決してソルバーのコストによるものではなく、求められる精度と速度が、向いていない、ということに尽きます。





Deterministic concurrent LP optimizer: primal and dual simplex
Showing first log only...

Root simplex log...
Iteration    Objective       Primal Inf.    Dual Inf.      Time
       0    2.3065000e+04   1.830000e+02   6.010239e+08     17s
   24989    5.9105058e+04   0.000000e+00   5.427999e+06     20s
   39027    1.4139465e+04   0.000000e+00   1.530505e+06     25s
   48531    8.4548149e+03   0.000000e+00   8.561291e+05     30s
   54075    4.6553869e+03   0.000000e+00   6.203191e+05     35s
   57243    4.0333315e+03   0.000000e+00   1.884978e+06     40s
   59619    3.2945051e+03   0.000000e+00   2.485297e+07     45s
   61995    2.8932136e+03   0.000000e+00   1.937645e+06     50s
   63843    2.6364303e+03   0.000000e+00   1.824680e+06     56s
   65955    2.4071407e+03   0.000000e+00   1.529677e+06     60s
   67803    2.1433875e+03   0.000000e+00   3.572679e+06     66s
   69387    2.0198157e+03   0.000000e+00   1.500083e+06     70s
   70957    1.8682992e+03   0.000000e+00   5.175105e+06     75s
   72527    1.7109733e+03   0.000000e+00   1.534901e+06     80s
   74371    1.6059518e+03   0.000000e+00   7.316991e+05     86s
   75691    1.4715193e+03   0.000000e+00   8.885731e+05     90s
   77275    1.2998909e+03   0.000000e+00   2.408987e+06     96s
   79123    1.2171491e+03   0.000000e+00   1.039386e+06    100s
   80707    1.1319239e+03   0.000000e+00   7.554920e+06    105s
   82555    1.0430034e+03   0.000000e+00   2.797781e+06    111s
   83875    9.5441597e+02   0.000000e+00   4.827466e+06    115s
   85459    8.9434760e+02   0.000000e+00   2.612262e+05    121s
   86779    8.2570058e+02   0.000000e+00   1.466299e+06    125s
   88363    6.7444245e+02   0.000000e+00   1.998739e+06    131s
   89683    5.7750613e+02   0.000000e+00   1.569387e+06    136s
   90999    5.1294778e+02   0.000000e+00   8.648063e+05    141s
   92031    4.6633167e+02   0.000000e+00   1.271406e+07    145s
   93329    4.1456737e+02   0.000000e+00   4.761322e+06    151s
   94349    3.7612396e+02   0.000000e+00   1.849774e+06    155s
   95599    3.2109644e+02   0.000000e+00   3.595911e+05    161s
   96629    2.6097565e+02   0.000000e+00   5.134349e+05    165s
   97893    2.2486428e+02   0.000000e+00   4.157836e+05    171s
   98907    1.7423268e+02   0.000000e+00   1.301501e+06    176s
  100199    1.2653451e+02   0.000000e+00   1.601937e+06    181s
  101199    8.5595718e+01   0.000000e+00   5.010955e+05    186s
  102247    4.7167686e+01   0.000000e+00   1.260490e+06    190s
  103487    1.2204544e+01   0.000000e+00   4.461667e+05    196s
  104407   -1.6047682e+01   0.000000e+00   1.948257e+05    200s
  105607   -4.7594571e+01   0.000000e+00   2.135647e+05    206s
  106527   -6.6654211e+01   0.000000e+00   1.916288e+05    211s
  107407   -8.9912197e+01   0.000000e+00   4.649965e+05    215s
  108547   -1.1011925e+02   0.000000e+00   2.579404e+06    221s
  109477   -1.2357405e+02   0.000000e+00   1.109971e+05    226s
  110437   -1.4304921e+02   0.000000e+00   4.081576e+06    231s
  111387   -1.5994959e+02   0.000000e+00   3.459370e+05    235s
  112567   -1.7748868e+02   0.000000e+00   4.569213e+05    241s
Concurrent spin time: 0.00s
Solved with dual simplex
Root relaxation: objective -6.890137e+02, 85445 iterations, 227.18 seconds
Total elapsed time = 401.32s
Total elapsed time = 476.00s
Total elapsed time = 579.92s
Total elapsed time = 672.39s
    Nodes    |    Current Node    |     Objective Bounds      |     Work
 Expl Unexpl |  Obj  Depth IntInf | Incumbent    BestBd   Gap | It/Node Time
     0     0 -689.01374    0 3777 1429275.00 -689.01374   100%     -  767s
H    0     0                    31485.000000 -689.01374   102%     -  768s
H    0     0                    27825.000000 -689.01374   102%     -  768s
H    0     0                    8355.0000000 -689.01374   108%     -  769s
     0     0 -578.43551    0 5449 8355.00000 -578.43551   107%     -  886s
H    0     0                    6115.0000000 -578.43551   109%     -  888s
     0     0 -574.51017    0 5343 6115.00000 -574.51017   109%     -  910s
     0     0 -574.34337    0 5278 6115.00000 -574.34337   109%     -  913s
     0     0 -574.34337
投稿者 時刻: 0 件のコメント:

2020年4月21日火曜日

NEOS SERVERの壁

NEOS　SERVERは、16MBの壁があります。今までMPSファイルをUploadしていたのですが、少し大きいインスタンスを行おうとするとこの壁に阻まれてしまいます。（最近は、CPLEXも開発者用というのがあって、月額3万程度で使うことができますが）　

最近、MPSファイルの代わりにLPファイルを使う事ができることに気付きました。LPファイルは、MPSに比べれば少ないファイルサイズになりますから、これで、かなりのインスタンスをチェックできることになります。また、Short Priorityのチェックを入れなければ、最長8時間？まで、計算してくれて結果をE-mailで得ることが出来ます。

で、やってみたらLPファイルとMPSファイルで目的関数値が異なる結果になってしまいました。ちょうど目的関数値の定数項の分だけ違いました。

宮代先生のWEB　
http://web.tuat.ac.jp/~miya/ipmemo.html
で、その辺の解説がありました。１０．LP ファイルで目的関数に定数項を含めたい
ということで、どうもLPファイルは、目的関数に定数を入れられないようです。

LPファイルをいじるのは、自信がないので、MPS・LPファイル両方生成させて、MPSファイルの常数項、例えば、
RHS
    RHS       OBJROW     -3900080.     R0000000  1.         
の項を結果からLPファイル結果から引き算することにしました。

以上で、State　Of　Art　SolverであるCPLEX/GUROBIとSC3の比較を行う準備が出来ました。

最適化汎用ソルバーは、今世紀に入ってからも格段の進歩をしています。
https://symposia.cirrelt.ca/system/documents/000/000/111/Bixby_original.pdf?1441306917
https://www.orsj.or.jp/archive2/or59-01/or59_1_11.pdf

(この時点で、SCIPのソース行数が50万行というのは、凄いです。GCC並みです。ちなみにSC3の行数は、ライブラリを含めても20万行程度ではないかと思います。SC2は、2-3万行です。SystemVerilog Simulatorは、自力で20万行を超えたところで挫折しました。）

それにも関わらず、ナーススケジューリング専用のソルバーSC3が必要となる理由を明らかにしていきたいと思います。

投稿者 時刻: 0 件のコメント:

2020年4月20日月曜日

土曜日のみ夜勤可

これも二つの方法があります。

前回やったように、夜勤不可というラベルを作って、土曜日以外の全てにそのラベルで予定を埋めてしまいます。これにより、残った予定を入れていない土曜日のみが、夜勤が入る可能な箇所となります。

もう一つの方法は、制約で入れてしまう方法です。

上記で似た制約があるので、それに習って制約を書けばよいです。
土曜日に夜勤可　→土曜日以外は、夜勤不可とすればよいですね。
さらに、先月分で、この制約を守っていないとエラーとなる可能性があるので、制約は、今月のみに効くようにする方がBetterです。よって、「今月の土曜日以外」というDay集合を作ります。
また、当該スタッフグループについても定義する必要があります。従って

Day集合:今月土曜日以外
グループ集合：土曜夜勤のみ可能

という二つの集合を新たに定義して、夜勤パターンを禁止にすればよいです。

 
 
 
操作動画はこちら、
https://www.nurse-scheduling-software.com/publications/video/add_night_shift_on_Sat_only.AVI
投稿者 時刻: 0 件のコメント:

2020年4月19日日曜日

木曜残り番が出来ないスタッフがいる


■考え方　2つの方法があります

　■残禁止というラベルを作って木曜の予定で入れてしまう　

　■制約で入れてしまう

　 

■制約化するかどうかは、他の人も使うことがあるかどうかです。制約化することは手間ですので、その手間に見合うかどうかが判断材料になります。
 

ラベルによる方法の動画は、以下です。

■考え方　
　■残ｘと表記させるラベルを定義します

 
　■木曜日に残ｘを入力

 
投稿者 時刻: 0 件のコメント:

2020年4月18日土曜日

ソフトエラーの対処方法

サポート事例から。
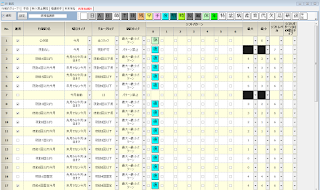
夜勤2人のところ、夜勤３人の箇所(黄色）があります。Why?　

エラーには、必ず理由があります。ソルバーは、目的関数値（重みペナルティの総和）が最小となるように作用します。そうなる原因は、必ずあります。

原因を調べるために、該当制約を見ます。
制約タイプは、ソフトスタッフ数最大最小になっています。この制約タイプは、
最大：ソフトレベル１
最小：ソフトレベル７
となっています。レベル７は、優先度最強、レベル1は、優先度最小です。つまり、2人より上回る側（最大）の優先度は、もっとも低いレベルになっています。大体、制約による結果というのは、両方の側のせめぎありによる戦いあるいは妥協の産物です。一方の側だけの制約というのは殆どありません。ある現象が出たら、そう至らしめる何かがあるはずです。

一方、行制約を見ると
個人ごとに夜勤回数設定が違うために、色々な制約が並んでいますが、大方ソフトレベルは６になっています。しかも、最小回数を規定しているので、夜勤回数最小指定は、日々の夜勤スタッフ数を上げる側に作用します。

まとめると
列制約最大規定　　　　　　　2人　ソフトレベル１　2人を上回る側にペナルティ重み
行制約夜勤回数最小規定　X人　ソフトレベル6　最小回数を下回る側にペナルティ重み
が発生することになります。この重みは、


具体的に重みは、列制約：１で10、行制約：６で1000の重みが与えられています。
各スタッフの最小夜勤回数を守る方が、夜勤スタッフ数2を破るよりペナルティがが少なく手済みます。ソルバーは、ペナルティ和が最小になる方を躊躇無く選択します。つまり、今回の現象は、優先度の違いによるものです。

不思議なのは、今までこの制約でやってきて、この現象は出たことはありません。なぜ、今月だけ、出たのでしょうか？
実は、今月から不足していたスタッフが充足したそうです。結果、人余りの方向に生じたということです。

解決策は、ソフト制約レベルは、最大最小共レベル７にすることです。
制約タイプを通常タイプに変更することで、最大最小ともレベル７に作用します。

修正後は、上記のように2人になりました。別な解決方法としては、行制約の最小人数を調整することでも可能ですが、クライアントの意図として、上記制約の方が適切である、ということです。

初期の制約設定は、私が勝手に設定したものですが、何ヶ月かやっていると上記のような細かい
調整が必要な箇所が出てきます。最低3ヶ月の期間を頂いているのは、このようにブラシュアップする期間が必要な為です。

以上の操作動画は、次です。
https://www.nurse-scheduling-software.com/publications/video/address_soft_error.AVI




投稿者 時刻: 0 件のコメント:

2020年4月14日火曜日

Python Editor Space Color

半角スペースは、オレンジにすることにしました。残念ながら全角に色はつけられません。
次回リリースで適用します。
投稿者 時刻: 0 件のコメント:

2020年4月13日月曜日

集合の包含関係を理解する

ここで、「土日連続休み」が達成されていれば、土日に限らない「連続休み」は自動的に達成されます。同様に、「土日連続休みの前に夜勤がない」が達成されていれば、「土日連続休み」は、自動的に達成されます。

これは、まさに、AならばBの関係です。Aは、Bの特殊形です。このとき、Bは、Aであるための必要条件、Aは、Bであるための十分条件となります。忘れたら、https://mathtrain.jp/conditions

包含関係で、含まれる方は、特殊形であり、制約はより厳しくなることから、より達成しにくくなります。達成しにくい方の制約レベルの方を高くすることは、包含する側の一般化制約にとっては、自動的に満たされるのでソフト制約レベルを設定する意味がありません。ですから、特殊になるにつれてレベルを低くすることが自然だと思います。逆に言うと、制約レベルを設定するには、集合の包含関係を理解していないと、リーズナブルな設定は難しいということになります。

連続休み設定のビデオは、https://nurse-scheduling-software.com/publications/video/consecutive_holidays.AVI

投稿者 時刻: 0 件のコメント:

2020年4月12日日曜日

COPT1.03を評価してみた

ライセンスのセットアップが面倒で、コマンドラインがなく、シェルで動くことに戸惑いました。テストインスタンスは、以前と全く同じで、CLP・HiGHs　Simplex・HiGHs　IPXとの比較を行いました。

結果は、公表しませんが、CLPよりは、遥かに出来が悪かったです。

これは、ジュリアンホール教授からも指摘を受けていますが、私のインスタンスはUnlike（あまり見かけない）インスタンスによることが大きいと思います。スプレッドシート結果を送ったら、その辺の言い訳はせず丁寧な説明をして頂いたことに好感が持てました。

エッセンスは、二つあり、ジュリアンホール教授が指摘していたようなIdiot　Crashによるもの、もう一つは、搭載しているのは、Dual　SimplexのみでPrimal　Simplexは搭載していないこと、ということでした。次期以降、Primal　Simplexも搭載し、CLPよりも速くなると言明されていました。将来的には、BarriorSolverも搭載するとのことでした。（大規模では、BarriorSolverの方がいいよとアドバイスを頂きました。ジュリアンホール教授は、InteriorPointと言っていたのですが、学術用語的には、同じと理解していますが違いがあるものでしょうか？）

いずれにしても、最適化を支える王道とも言うべき線形ソルバーの匠達と、直接にやり取りさせて頂き光栄でした。私の作ったベンチマークが少しでも今後の最適化技術の発展に貢献できたらと思います。（私にしても、線形ソルバーの性能向上が、自動的にNSP世界記録が更新できる可能性をもたらすのでメリットがあります。）
投稿者 時刻: 0 件のコメント:

2020年4月11日土曜日

祝日日勤分だけ代休

①祝日の勤務で日勤であれば回数分代休をふる ②祝日夜勤であれば代休なし という制約のリクエストがありました。既に何回か同種の記述は、このブログでも紹介していますが、改めてチュートリアル１１に追加する方法をビデオにしました。

Pythonコードは以下です。 
import sc3
def 代休処理():
    for person in 全スタッフ:
        祝日日勤list=[]
        代休list=[]
        for day in 今月:
            if day in 休日:
                v=sc3.GetShiftVar(person,day,'代休')#休診日は代休禁止
                sc3.AddHard(~v,'休日代休禁止')#ハード制約
            else:
                v=sc3.GetShiftVar(person,day,'代休')#休診日以外の代休
                代休list.append(v)#数をカウント
            if day in 祝日:
                v=sc3.GetShiftVar(person,day,'日勤')#祝日日勤
                祝日日勤list.append(v)#数をカウント
        s='祝日日勤数と代休数は等しい'
        sc3.AddHard(sc3.SeqComp(祝日日勤list,代休list),s)#ハード制約
代休処理()

この代休を日勤扱いとするには、新たに日勤集合として次のように定義します。
この日勤集合というシフトについて、今までの「日勤」で制約した制約を「日勤集合」というシフトに
置き換えれば、代休も含めた日勤集合について制約が作用することになります。
投稿者 時刻: 0 件のコメント:

2020年4月10日金曜日

AならばBについて

二つの条件 p 、q に対して、「 p を満たすものは全て q も満たす 」 というとき、「 p は q である為の十分条件である 」 あるいは 「 q は p である為の必要条件である 」 という。また、「 p は q である為の十分条件であり、q は p である為の十分条件である 」 というとき、「 p は q である為の必要十分条件である 」 あるいは 「 p と q とは同値である 」 という。 となっています。
この辺、中々面倒なので、こちらが参考になります。 https://mathtrain.jp/conditions

AならばB（A→B)を論理で表現すると
~A |B
となります。これは、AがTrueとすると~AはFalse、よってBがTrueとなることが必然となることから理解できます。

反対方向、B→Aは、
~B|A
となります。必要にして十分、同値の関係は、上記が、同時に成立することですから
~A|B & A|~B
となります。よって、同値制約は、以下の通りとなります。


def 等号制約(a,b,s):
    sc3.AddHard( (a|~b) &(~a|b),s)
投稿者 時刻: 0 件のコメント:

2020年4月9日木曜日

土日夜勤した場合10日Window内で公休を1日取得2日ある場合はその月内でもう1日取得

実は、前に実装した土日夜勤した場合前後の3日間で代休を取る　が破綻してしまいました。1年を通してシミュレーションしてみると2021年5月の連休で物理的に取得不可能なことが判り、クライアントに1ヶ月3分割することを提案しました。で、出てきた仕様が次です。
■土日夜勤の場合、公休が２日取得となりますが　そのうち１日は必ず「１か月を３分割し、そのWindow以内に公休を消化する」にし、もう１日は同月内であれば、いつでも良いとする。もちろん、金土夜勤の場合、日月夜勤の場合は今まで通り「１か月を３分割し、そのWindow以内に公休を消化する」こととする。
■仕様の背景は、理解していません。とりあえず、実装し易い形に変形しています。 以下をPythonで実装しています。 土日夜勤した場合10日Window内で公休を1日取得2日ある場合はその月内でもう1日取得()
ここでの、ポイントは、公休(代休)が取得される論理です。例えば、A　Window期間中に土日のどちらか夜勤があれば、A　Window中、公休は必ず1個取得されます。これが、Ac==Aa|Ab　部になります。さらに、B　Window中に土日連続夜勤があったとき(Bab)　A Window で公休が発生するというロジックです。夜勤数、公休数共に、2個以下に制限してあるので、この条件が発生するのはAc==Babでしか起こりえません。 また、公休が発生しないのは、(Aa|Ab|Bab) のどれも該当しない、つまり夜勤が発生しないときは、公休を生成させないということに符合します。 ということで、簡単なロジックで、必要にして十分、つまり同値であることが判ります。同値のルーチンは、前々回に説明しました。また、Acや、Acは、ΣXi>=1　という関係です。これは、前回説明しました。それぞれのWindow内でORを取ればよいことが判ります。　同様にして、他のWindowも処理できます。 かなり複雑な仕様ですが、Pythonで100行足らずで記述できました。かなり難しい部類のプログラムだと思いますが、SeqCompや、SeqExpr等の制約関数を使っていないので、性能的にもMaxになっているはずです。

a:土夜 b:日夜
c:公休(土日以外）
A:Window1 B:Window2 C:Window3
Ac== (Aa| Ab |Bab)
Bc== (Ba| Bb |Cab)
Cc== (Ca| Cb |Aab)
Σ(a|b)<=2 今月
Σc<=2 今月 

def 等号制約(a,b,s):
    sc3.AddHard( (a|~b) &(~a|b),s)
 
def 代休window処理_v2(person,window):
    holiday_domain=[]
    sat_sun=[]
    ss=[]
    for day in window:
        if day in 土 or day in 日:
            sat_sun.append(day)
        else:
            holiday_domain.append(day)
        if day in 土 and day+1 in window:
            ss.append(day)
    
    vreturn_list=[]
    vsat_sun=[]
    vholidays=[]
    vssdays=[]
    for day in ss:
         #sc3.print('土'+str(day)+'\n')
         v1=sc3.GetShiftVar(person,day,'入り')#
         v2=sc3.GetShiftVar(person,day+1,'明け')
         vssdays.append(v1&v2)#土日連続夜勤

    for day in sat_sun:
         #sc3.print('土'+str(day)+'\n')
         v1=sc3.GetShiftVar(person,day,'入り')#
         v2=sc3.GetShiftVar(person,day,'明け')
         vsat_sun.append(v1|v2)#土日に夜勤
    for day in holiday_domain:
         #sc3.print('H'+str(day))
         v1=sc3.GetShiftVar(person,day,'公休')#
         vholidays.append(v1)#公休
    s=staffdef[person]+daydef[day]+'代休処理'
    #sc3.AddSoft(sc3.SeqComp(vsat_sun,vholidays),s,7)
    vreturn_list.append(sc3.Or(vsat_sun))
    vreturn_list.append(sc3.Or(vholidays))
    vreturn_list.append(sc3.Or(vssdays))
    return vreturn_list
       


def 土日夜勤した場合10日Window内で公休を1日取得2日ある場合はその月内でもう1日取得():
    今月日数=len(今月)
    WindowDays=今月日数/3 #3分割
    win1=[]
    win2=[]
    win3=[]
    for day in 今月:
        if len(win1)<   WindowDays:
            win1.append(day)
        elif len(win2)< WindowDays:
            win2.append(day)
        else:
            win3.append(day)
    sc3.print('window1=',str(len(win1))+'\n')
    sc3.print('window2=',str(len(win2))+'\n')
    sc3.print('window3=',str(len(win3))+'\n')
    
    
    #今月で見たときに土日出勤数==公休数とする
    sat_sun=[]
    holiday_domain=[]
    for day in 今月:
        if day in 土 or day in 日:
            sat_sun.append(day)
        else:
            holiday_domain.append(day)

    for person in 夜勤可能:
        vsat_sun=[]
        vholidays=[]
        vlist1=代休window処理_v2(person,win1)#Window内では1日に限定
        vlist2=代休window処理_v2(person,win2)#Window内では1日に限定
        vlist3=代休window処理_v2(person,win3)#Window内では1日に限定
    
        for day in sat_sun:
            #sc3.print('土'+str(day)+'\n')
            v1=sc3.GetShiftVar(person,day,'入り')#
            v2=sc3.GetShiftVar(person,day,'明け')
            vsat_sun.append(v1|v2)
        for day in holiday_domain:
            #sc3.print('H'+str(day))
            v1=sc3.GetShiftVar(person,day,'公休')#
            vholidays.append(v1)
        s=staffdef[person]+daydef[day]+'今月処理'
       
        sc3.AddHard(sc3.SeqLE(0,2,vsat_sun),s+'土日')#土日夜勤は2回以内
        sc3.AddHard(sc3.SeqLE(0,2,vholidays),s)#公休2回以内
        等号制約(vlist1[0]|vlist2[2],vlist1[1],'Ac==(Aa|Ab|Bab)') 
        等号制約(vlist2[0]|vlist3[2],vlist2[1],'Bc==(Ba|Bb|Cab)') 
        等号制約(vlist3[0]|vlist1[2],vlist3[1],'Cc==(Ca|Cb|Aab)')
投稿者 時刻: 0 件のコメント:

2020年4月8日水曜日

ORは、ΣXi>=1

SAT上の論理和は、ΣXi>=1 です。つまり、OR演算で、ΣXi>=1が計算できることになります。
これを利用して、加算器を使わずに計算ができることがあります。

反対にΣXi<=1は、どうなるでしょうか？　これは、全ての2個の加算がXi+Xk==2となる全ての組み合わせを禁止すればよいです。これには、ｎC2個分の節を要します。　

それでは、ΣXi==1は、どうなるでしょうか？　ΣXi>=1 && ΣXi<=1　と制約すればよいことになります。

上記は、1でしたが、2,3...を想像してみてください。途端に組み合わせ爆発してしまうのが容易に想像できると思います。


投稿者 時刻: 0 件のコメント:

2020年4月7日火曜日

同値　⇔　とは

C言語的には＝＝、　論理学的には　⇔　です。　
 論理回路的には、XOR（排他的論理和）の否定になります。

命題 P命題 QP ⇔ Q
真真真
真偽偽
偽真偽
偽偽
真
 
命題 P命題 QP ⊻ Q
真真偽
真偽真
偽真真
偽偽偽

では、同値をどのように実装するかというと、排他的論理和の否定からすると
~(~P& Q| P&~Q)
=P&~Q & ~P&Q
となります。または、真理値表から、P＆Q|　~P&~Q でもよいですね。
これをPythonで記述すればよいです。
下のようになります。sは、制約名になります。排他的論理和も同様にして記述できます。
<基数制約の難しさ＞
ちなみにSAT界における基数制約（OR界における基本制約である線形加算不等式制約）も、AND　OR　NOTを用いて、理論的には記述可能です。やってみれば直ぐわかるのですが、加算器というのは、論理回路で普通に合成すると排他的論理和XORのSeaofGatesで、とんでもない量の加算器が必要になります。この原因は、組み合わせ解空間がとんでもなく広いということにあります。ですから基数制約を記述するには、用意されている専用の制約関数を用いることになります。しかし、専用の制約関数はあるのですが、それを用いるからといって、そもそもの組み合わせ解空間が狭くなる訳ではありません。依然としてそのままあります。ですから、基数制約を記述しなくて済むならば、そちらがベターです。
＜UnitPropagation＞
SAT界では、UnitPropagationが重要ですが、EXOR系（同値も）の記述では、これが上手くいきません。ですので、次のような記述の順序が推奨されます。

EXORを含まない論理記述　> 基数制約> EXOR系

下の記述を用いて、かなり難しい制約例を紹介するのですが、あと一回背景知識が必要となります。

def 等号制約(a,b,s):
    sc3.AddHard( (a|~b) &(~a|b),s)
投稿者 時刻: 0 件のコメント:

2020年4月3日金曜日

土日の日準を禁止

休みの連続勤務を禁止する制約ですが、GUIで書けます。日準パターンを禁止にすればよいのですが、最初の日（日勤）を土曜日とすればよいです。よって、下のようになります。



投稿者 時刻: 0 件のコメント:

2020年4月2日木曜日

休みの数だけ公休取得

月毎に公休数が変わる職場が多いと思いますが、各月毎に公休数を設定するのが面倒という方のためのスニペットが以下になります。今月の休診日数を取得して、同じ数だけ、公休数を取得するという制約になります。


import sc3
def 今月休診日数():
    休診日数=0
    for day in 全日:
        if day < 制約開始日:
            continue
        if day in 休日:
            休診日数+=1
    return 休診日数

def 休診日の数だけ公休を取る():
    休診日数=今月休診日数()
    for person in 全スタッフ:
        vlist=[]
        for day in 今月:
            v1=sc3.GetShiftVar(person,day,'公休')
            vlist.append(v1)
        s='公休数を休診日数だけ取る '+staffdef[person]
        sc3.AddHard(sc3.SeqLE(休診日数,休診日数,vlist),s)

休診日の数だけ公休を取る()
投稿者 時刻: 0 件のコメント:

2020年4月1日水曜日

最新論文で言及

[45] T.Sugawaraとして、 IntelのNadelさんの最新論文で言及されています。これで、3-4度言及されています。
https://ieeexplore.ieee.org/abstract/document/8894273

なるほど、そういう考え方もありますが、私は別なアプローチで改善することにしました。
SAT系については、大体やり尽くした感があったのですが、今少し改善の余地があることに気付きました。次のリリースに向けて実装してみようと思います。
投稿者 時刻: 0 件のコメント:
登録: 投稿 (Atom)